Математическая модель солнечной батареи

Изучение энергетических процессов в автономных системах электроснабжения с помощью компьютерного имитационного моделирования. Суть математической модели солнечной батареи, описываемой вольтамперной характеристикой при заданной освещенности и температуре.

Рубрика	Коммуникации, связь, цифровые приборы и радиоэлектроника
Вид	реферат
Язык	русский
Дата добавления	11.09.2016
Размер файла	299,9 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

«Дагестанский Государственный Технический Университет»

по дисциплине: «Основы математического моделирования»

на тему: «Математическая модель солнечной батареи»

Махачкала 2016 г

1. Что такое математическая модель

2. Математическая модель солнечной батареи

Заключение

Список используемой литературы

Фотоэлектрические генераторы для прямого преобразования энергии излучения Солнца в электрическую энергию, собранные из большого числа последовательно соединенных фотопреобразователей солнечных элементов (СЭ), получили название солнечных батарей (СБ). Современные солнечные батареи генерируют на свету значительную электрическую мощность и применяются как для питания космических аппаратов (КА), так и для многих наземных автономных устройств различного назначения.

Солнечные батареи состоят из десятков и сотен тысяч отдельных СЭ, соединенных параллельно-последовательно с целью обеспечения требуемых номиналов тока и напряжения.

В данном реферате рассмотрена математическая модель солнечной батареи. Эта модель, описываемая вольтамперной характеристикой (ВАХ) при заданной освещённости и температуре является базовой для расчета энергии СБ.

1. Что такое математическая модель

Модель в широком смысле — это любой образ, аналог мысленный или установленный изображение, описание, схема, чертеж, карта и т. п. какого либо объема, процесса или явления, используемый в качестве его заменителя или представителя. Сам объект, процесс или явление называется оригиналом данной модели.

Моделирование — это исследование, какого либо объекта или системы объектов путем построения и изучения их моделей. Это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.

На идее моделирования базируется любой метод научного исследования, при этом, в теоретических методах используются различного рода знаковые, абстрактные модели, а в экспериментальных — предметные модели.

При исследовании сложное реальное явление заменяется некоторой упрощенной копией или схемой, иногда такая копия служит лишь только для того чтобы запомнить и при следующей встрече узнать нужное явление. Иногда построенная схема отражает какие-то существенные черты, позволяет разобраться в механизме явления, дает возможность предсказать его изменение. Одному и тому же явлению могут соответствовать разные модели.

Задача исследователя — предсказывать характер явления и ход процесса.

Иногда, бывает, что объект доступен, но эксперименты с ним дорогостоящи или привести к серьезным экологическим последствиям. Знания о таких процессах получают с помощью моделей.

Важный момент — сам характер науки предполагает изучение не одного конкретного явления, а широкого класса родственных явлений. Предполагает необходимость формулировки каких — то общих категорических утверждений, которые называются законами. Естественно, что при такой формулировке многими подробностями пренебрегают. Чтобы более четко выявить закономерность сознательно идут на огрубление, идеализацию, схематичность, то есть изучают не само явление, а более или менее точную ее копию или модель. Все законы — это законы о моделях, а поэтому нет ничего удивительного в том, что с течением времени некоторые научные теории признаются непригодными. Это не приводит к краху науки, поскольку одна модель заменилась другой более современной.

Особую роль в науке играют математические модели, строительный материал и инструменты этих моделей — математические понятия. Они накапливались и совершенствовались в течение тысячелетий. Современная математика дает исключительно мощные и универсальные средства исследования. Практически каждое понятие в математике, каждый математический объект, начиная от понятия числа, является математической моделью. При построении математической модели, изучаемого объекта или явления выделяют те его особенности, черты и детали, которые с одной стороны содержат более или менее полную информацию об объекте, а с другой допускают математическую формализацию. Математическая формализация означает, что особенностям и деталям объекта можно поставить в соответствие подходящие адекватные математические понятия: числа, функции, матрицы и так далее. Тогда связи и отношения, обнаруженные и предполагаемые в изучаемом объекте между отдельными его деталями и составными частями можно записать с помощью математических отношений: равенств, неравенств, уравнений. В результате получается математическое описание изучаемого процесса или явление, то есть его математическая модель.

Изучение математической модели всегда связанно с некоторыми правилами действия над изучаемыми объектами. Эти правила отражают связи между причинами и следствиями.

Построение математической модели — это центральный этап исследования или проектирования любой системы. От качества модели зависит весь последующий анализ объекта. Построение модели — это процедура не формальная. Сильно зависит от исследователя, его опыта и вкуса, всегда опирается на определенный опытный материал. Модель должна быть достаточно точной, адекватной и должна быть удобна для использования.

2. Математическая модель солнечной батареи

Для анализа энергетических процессов в автономных СЭП в настоящее время целесообразно использовать методы компьютерного имитационного моделирования. Это позволяет оценить:

— обеспечение энергобаланса в автономных СЭП при известных энергетических характеристиках основных и буферных источников энергии и временной диаграмме энергопотребления со стороны нагрузки;

— влияние энергетических характеристик СЭП на обеспечение энергобаланса в системе в условиях временных изменений энергетических характеристик источников электропитания;

— влияние на энергетические характеристики СЭП таких параметров, как освещённость солнечной батареи, температура, время года, и т.п.

Для проведения анализа необходимо разработать математическую модель солнечной батареи.

Модель солнечной батареи

Рисунок 1 — Схема замещения солнечного элемента

где — ток через внешнюю нагрузку, — обратный ток насыщения, q — заряд электрона, Т — абсолютная температура, °К, k — постоянная Больцмана, — напряжение на выходе элемента, — ток неосновных носителей, генерированных светом (фототок).

Влияние освещённости СЭ на величину выражается формулой

где W — освещённость СЭ.

Реализуем математическую модель СЭ. В качестве примера выберем СЭ со следующими характеристиками: = 0,55 В, = 5,5 A. => .

Схема, реализующая ВАХ солнечного элемента, описываемого выражением (1), приведена на рисунке 2. Она позволяет оценить влияние на работу СЭ таких параметров, как уровень освещённости СЭ (номинальное значение W=1360 кВт/), температура окружающей среды (номинальное значение K=298 K), а также угол падения светового потока (номинальное значение б=90° = р/2 рад).

Рисунок 2 — Математическая модель СЭ

Рисунок 3 — Характеристики СЭ, описываемые уравнением (2)

а — вольтамперная характеристика, б — вольтваттная характеристика

Протестируем солнечную батарею, состоящую из 3 элементов соединённых последовательно. В этом случае напряжение на выходе СБ определяется по формуле , где N — количество солнечных элементов, соединённых последовательно;

На рисунке 4 изображена модель СБ, состоящая из 3 СЭ, соединённых последовательно. электроснабжение солнечный батарея вольтамперный

Рисунок 4 — Модель солнечной батареи, состоящей из 3 солнечных элементов, соединённых последовательно

Рисунок 5 — Характеристики схемы, приведённой на рисунке 4

а — вольтамперная характеристика, б — вольтваттная характеристика

Как видно из рисунка 5, напряжение холостого хода СБ в 3 раза больше напряжения холостого хода СЭ (см. рисунок 3) => модель составлена, верно.

Протестируем солнечную батарею, состоящую из 2 элементов соединённых параллельно. В этом случае напряжение на выходе СБ определяется по формуле

где М — количество солнечных элементов, соединённых параллельно.

Рисунок 6 — Характеристики схемы, состоящей из 2 солнечных элементов

а — вольтамперная характеристика, б — вольтваттная характеристика

Как видно из рисунка 6, ток короткого замыкания СБ в 2 раза больше тока короткого замыкания СЭ (см. рисунок 3) => модель составлена верно

Рассмотрим модель солнечной батареи, состоящей из 6 солнечных элементов, соединённых последовательно-параллельно.

В этом случае напряжение на выходе СБ определяется по формуле

где N — количество солнечных элементов, соединённых последовательно

где М — количество солнечных элементов, соединённых параллельно.

а — вольтамперная характеристика, б — вольтваттная характеристика

Рисунок 7 — Характеристики схемы, состоящей из 6 элементов, соединённых последовательно-параллельно

Заключение

Солнечные элементы и батареи представляют собой сложный для исследований объект, свойства которого зависят от множества факторов. На электрические характеристики СБ сильное влияние оказывают параметры окружающей среды, свойства материала, из которого изготовлены СЭ, технологические особенности СЭ и конструктивные параметры батарей. Прогнозирование характеристик СБ представляет собой достаточно сложную задачу, для решения которой используется моделирование. Существующие модели солнечных батарей не принимают во внимание всех факторов, влияющих на энергетические характеристики СБ.

Разработанная математическая модель солнечной батареи позволяет оценить влияние на характеристики солнечной батареи как внутренних факторов (Uxx, Ikz), так и внешних (W, T, б). Модель предназначена для проектирования СЭП. Результаты тестирования модели подтверждают её работоспособность.

Список используемой литературы

1. Бакулин Д. В., Борзых С. В., Ососов Н. С., Щиблев Ю. Н., “Моделирование процесса раскрытия солнечных батарей”, Матем. моделирование, 2004.

2. Бордовский Г. А., Физические основы математического моделирования [Текст] : учеб. пособие для студ. физико-матем. спец. вузов / Г.А. Бордовский, А.С. Кондратьев, А.Д.Р. Чоудери. — М.: Академия, 2005.

3. Бушуев А. Ю. , Фарафонов Б. А., “Математическое моделирование процесса раскрытия солнечной батареи большой площади”, Мат. моделир. и числ. методы, 2014, № 2, 101-114.

4. Макарова Н.А. Основные этапы моделирования. — СПб.: Питер, 2005

5. Самарский А. А., Математическое моделирование: Идеи. Методы. Примеры / А. А. Самарский, А. П. Михайлов. — 2-е изд., испр. — Москва: Физматлит, 2009.

Размещено на Allbest.ru

Подобные документы

Разработка дискретного регулятора мощности секционированной солнечной батареи, входящего в состав энергопреобразующей аппаратуры, в части системы управления шунтирующими коммутаторами, для обеспечения требуемого качества выходного напряжения КЭП.

дипломная работа [2,1 M], добавлен 27.07.2012

Рассмотрение особенностей солнечных элементов и выбор типа солнечной панели. Анализ типовых схемотехнических и конструкторских решений контроллеров заряда аккумуляторной батареи. Разработка структурной и электрической схемы, конструкции устройства.

дипломная работа [4,7 M], добавлен 10.10.2015

Схема солнечной фотоэлектрической установки. Выбор электродвигателя и определение передаточных функций. Моделирование системы автоматического управления средствами MATLAB. Подбор микроконтроллера, драйвера двигателя и датчика уровня освещенности.

курсовая работа [7,0 M], добавлен 11.08.2012

Расчет переходного процесса на основе численных методов решения дифференциальных уравнений. Разработка математической модели и решение с использованием метода пространства состояний. Составление математической модели с помощью матрично-векторного метода.

курсовая работа [161,1 K], добавлен 14.06.2010

Расчет емкости аккумуляторных батарей. Буферная система электропитания с ВДК. Минимально допустимый уровень напряжения при разряде аккумуляторной батареи с учетом минимального уровня напряжения на одном элементе. Определение коэффициента отдачи батареи.

контрольная работа [142,3 K], добавлен 04.04.2013

Анализ и выбор системы электропитания и определение числа элементов аккумуляторной батареи. Расчет и выбор емкости аккумуляторной батареи. Определение числа вольтдобавочных конвертеров в ЭПУ. Выбор типа и материала магнитопровода для трансформатора Т1.

контрольная работа [116,1 K], добавлен 01.05.2019

Анализ существующих методов реализации системы контроля параметров линейной батареи. Общая характеристика системы Siemens PSS400. Обоснование языка программной реализации. Разработка контроллера интерфейса USB 2.0. Модули обработки и упаковки данных.

дипломная работа [4,4 M], добавлен 30.12.2010

Источник

Моделирование характеристик солнечного модуля

Рубрика: Технические науки

Дата публикации: 26.12.2016 2016-12-26

Статья просмотрена: 1161 раз

Библиографическое описание:

Лысенко, В. С. Моделирование характеристик солнечного модуля / В. С. Лысенко, А. А. Гафаров, Г. С. Смородин. — Текст : непосредственный // Молодой ученый. — 2016. — № 29 (133). — С. 109-112. — URL: https://moluch.ru/archive/133/37357/ (дата обращения: 18.06.2021).

В данной статье представлена модель фотоэлектрического модуля, реализованная в среде Matlab. Модель основывается на уравнениях, описывающих вольт-амперные характеристики. Разработанная модель дает возможность исследовать вольт-амперные и ватт-вольтные характеристика фотоэлектрического модуля в зависимости от температуры и интенсивности солнечного излучения.

Ключевые слова: фотоэлектрический солнечный модуль, моделирование, вольт-амперные характеристики

За последние годы тенденция в использовании источников возобновляемой энергии резко возросла. Большое распространение, как в России, так и за рубежом получила солнечная энергия. Основными преимуществами солнечной энергии является: возобновляемость, обильность, постоянство, доступность, экологическая чистота, бесшумность, экономичность, инновационные технологии.

Из-за большого применения фотоэлектрических панелей появилась необходимость точного определения параметров и характеристик модулей. На практике, для изучения характеристик солнечных панелей широко применяется математическая модель, основанная на эквивалентной электрической схеме фотоэлектрического элемента и формуле полного тока солнечного элемента с единичной площади:

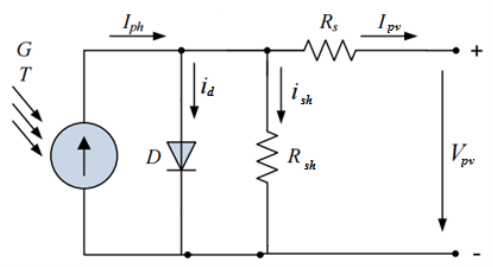
Рис. 1. Эквивалентная схема солнечного элемента

Характеристическое уравнение можно вывести непосредственно с помощью закона Кирхгофа:

,(1)

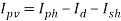
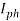
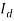
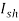
где – фототок, зависящий от плотности солнечного излучения, А;

– ток, протекающий через диод;

– ток, протекающий через шунтирующее сопротивление R_sh.

Ток, протекающий через диод, записывается следующим образом:

(2)

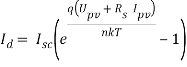
где – обратный ток насыщения диодов, А; q– заряд одного электрона (1,602 ∙ 10 -19 Кл); k – постоянная Больцмана (1,38 ∙ 10 -23 Дж/К); T – температура перехода в градусах Кельвина, К; n – коэффициент, зависящий от материала СЭ; – последовательное сопротивление, Ом; – шунтирующее сопротивление, Ом.

При помощи коэффициента n можно учесть свойства материала, который был применен при производстве солнечного элемента. Значения данного коэффициента может варьироваться от 1 до 2 (в некоторых случаях бывает более 2) и зависит от материала, из которого изготовлен элемент.

В свою очередь ток

(3)

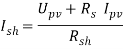
Зависимость между током фотоэлектрического элемента и напряжением на клеммах может быть описана уравнением следующего вида:

(4)

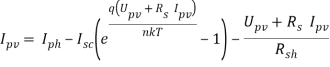
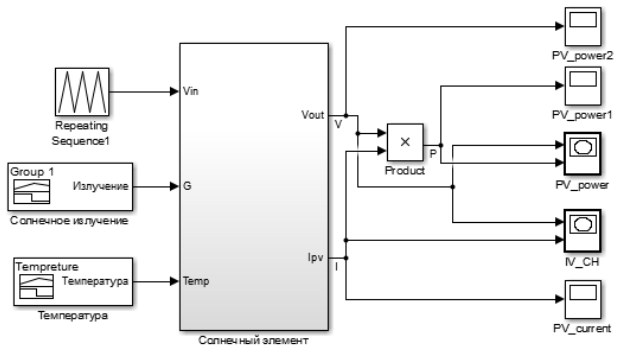
При помощи описанной выше математической модели можно изучить вольт-амперные характеристики определенных солнечных элементов. Для решения таких задач разумно использовать методы компьютерного программирования. Программный комплекс Matlab реализует принцип визуального программирования. Библиотека Simulink разработана специально для моделирования электрических процессов различной сложности. В ходе разработки модели воспользовались литературой [1, 2]. При помощи стандартных блоков реализуем модель солнечного элемента, она будет выглядеть следующим образом:

Рис. 2. Модель фотоэлектрического элемента в программном комплексе Matlab

Разработанная модель дает возможность фиксировать основные параметры солнечного модуля. При моделировании не учитывалась возможность частичного затемнения поверхности солнечного модуля. Это ограничение дает возможность применять классические аналитические выражения. На рисунках 3 и 4 представлены результаты моделирования.

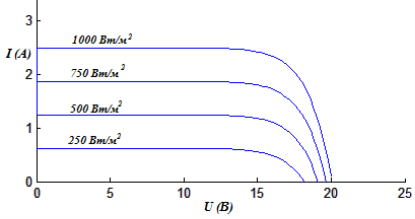
На рисунке 3 представлено семейство вольт-амперных характеристик при постоянной температуре 25 ˚С и изменяемом солнечном излучении от 250 до 1000 Вт/м2 с шагом 250 Вт/м2.

Рис. 3. Семейство вольт-амперных характеристик при различных уровнях солнечного излучения

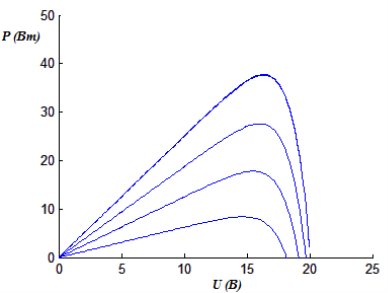
Кривые ватт-вольтных характеристик при аналогичных условиях моделирования можно увидеть на рисунке 4.

Рис. 4. Семейство ватт-вольтных характеристик при различных уровнях солнечного излучения

Реализованная модель фотоэлектрического модуля в среде Matlab в данной работе дает возможность исследования вольт-амперных и ватт-вольтных характеристик фотоэлектрического модуля в соответствии с изменяющимися параметрами окружающей среды.

1. Бордина Н. М. Моделирование вольт-амперных характеристик солнечных элементов и солнечных батарей [Текст] / Н. М. Бордина, В. А. Летин // Электротехническая промышленность. — М.: Информэлектро. — 1986. — 64 с.
2. Rodrigues E. M. G. et al. Simulation of a solar cell considering single-diode equivalent circuit model // International conference on renewable energies and power quality, Spain. — 2011. — С. 13–15.

Источник