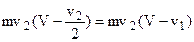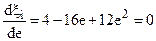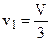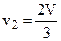Что такое идеальный ветряк

КЛАССИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ВЕТРЯКА

Теория идеального ветряка

Теорию идеального ветряка впервые разработал в 1914 г. В. П. Ветчинкин на основе теории идеального гребного винта. В этой работе он установил понятие коэффициента использования энергии ветра идеальным вет­ряком.

В 1920 г. проф. Н. Е. Жуковский изложил теорию «Ветряной мельницы НЕЖ», где сделал вывод коэффициента использования энергии ветра идеальным ветря­ком. Аналогичные теории были разработаны позднее также в нашей стране проф. Г.X. Сабининым и акад. Г.Ф. Проскура.

Теория идеального ветряка проф. Н.Е. Жуковского носит название классической теории, она устанавливает, что максимальный коэффициент использования энергии ветра идеальным ветряком равен 0,593. Наиболее полно, с точки зрения практического при­менения, теория идеального ветряка изложена проф. Г.X. Сабининым, согласно которой, коэффициент исполь­зования энергии ветра идеальным ветряком равен 0,687.

Идеальным ветряком называют ветроколесо, у которого:

1) ось вращения параллельна скорости ветра;

2) бесконечно большое число лопастей очень малой ширины;

3) профильное сопротивление крыльев равно нулю, и циркуляция вдоль лопасти постоянна;

4) потерянная скорость воздушного потока на ветроколесе постоянна по всей ометаемой поверхности ветряка;

5) угловая скорость стремится к бесконечности.

КЛАССИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ВЕТРЯКА

Представим равномерный поток ветра, набегающий на идеальное ветроколесо со скоростью Vв сечении АА’(рис.1). В сечении ВВ’на ветроколесе скорость будетV₁=V–v₁, а на некотором расстоянии позади ветряка в сечении СС‘ скорость будет V₂ = V – v₂.

При этом вращающееся ветроколесо создаст подпор, вследствие чего скорость потока, по мере приближения к ветряку и некоторое время за ветряком, падает, как показано кривой I на рис. 1

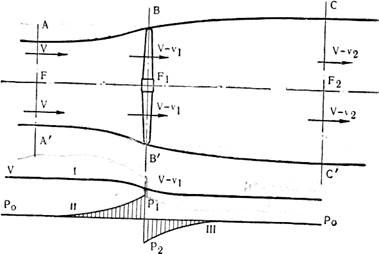
Вместе с этим давление воздуха р, по мере приближения к ветряку, повышается (кривая II ), и при прохождении через oметаемую по­верхность оно резко падает. За ветряком образуется не­которое разрежение р₀ – p₂, которое, по мере удаления от ветряка, ассимтотически приближается к нулю, т. е. восстанавливается нормальное давление (кривая III ). Потерю скорости за идеальным ветряком можно уста­новить при помощи уравнения Бернулли: 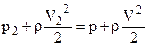. Так как Р₂ V₂.

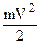
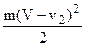
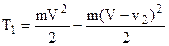
Кинетическая энергия ветра перед ветряком равна , а за ветряком . Разность этих энергий затрачена на ветроколесе и, в случае отсутствия потерь, может быть получена как полезная работа: (а)

Преобразовав правую часть уравнения (а), получим: 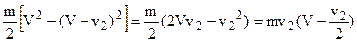. Следовательно: (б)

Энергию T₁, воспринятую ветроколесом, можно выра­зить как произведение из силы давления ветра Рна ско­рость в плоскости ветряка (V – v₁), т. е.: T₁= Р(V – v₁). (в)

Лобовое давление P равно приращению количества движения струи, проводящей через метаемую поверх­ность, т. е.: P = m v₂.

Подставляя значение Рв уравнение (в), получим T₁ = mv₂(V – v₁) (г).

Сравнивая уравнения (б) и (г) находим, что:

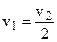
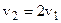
откуда: или: (1)

Равенство (1) показывают, что потеря скорости воз­душного потока происходит не только в сечении ветроколеса, но также и на некотором расстоянии за ветряком, причём полная потеря скорости в два раза больше потери на ветроколесе.

Через ометаемую поверхность Sветроколеса протекает масса воздуха m, количество которой за 1 секунду будет равно: m = rSV. (2)

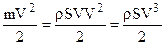
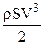
Подставляя значение массы воздуха в выражение кине­тической энергии ветра перед ветроколесом, получим: . Взяв отношение секундной работы, воспринятой иде­альным ветроколесом: T₁ = P×(V – v_l ) к той энергии ветра, которая протекала бы через сече­ние, равное ометаемой поверхности ветряка: ,

получим идеальный коэффициент использования энергии ветра x_i. 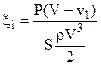(3)

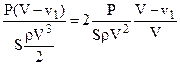
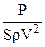
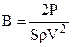
Преобразуем это уравнение: Выражение называют коэффициентом нагрузки на ометаемую площадь, или коэффициентом лобового давле­ния, и обозначают буквой В, т. е.: (4)

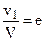
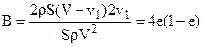
Подставив в это уравнение P = pS(V – v₁)v₂ = pS(V – v₁)2v₁и обозначив , после сокращений получим: (5)

Поступая так же с уравнением (3 66), для x_i. получим: 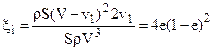(6)

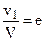
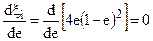
Отношение называют коэффициентом торможения. Определим значение е , при котором x_i будет иметь максимальную величину. Для этого возьмём первую про­изводную и приравняем её нулю, т. е.: или:

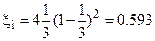
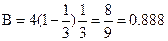
откуда: 3е 2 – 4е + 1 = 0. Решая это равенство, находим, что x принимает мак­симальное значение, когда e = 1/3, при этом Из уравнения (3) находим В –коэффициент нагрузки на ометаемую площадь при максимальном x_i: Таким образом, из классической теории идеального, ветряка вытекают следующие основные положения.

1. Максимальный коэффициент использования энергии ветра идеального ветроколеса равен x_i = 0,593.
2. Потеря скорости в плоскости ветроколеса равна одной трети скорости ветра:
3. Полная потеря скорости ветра за ветроколесом в два раза больше потери скорости в плоскости ветроко­леса:

Таким образом, скорость ветра за ветроколесом в три раза меньше скорости ветра перед ветроколесом.

1. Коэффициент нагрузки на ометаемую поверхность ветроколеса равен B = 0,888.

Е.M. Фатеев Задаваясь коэффициентом торможения 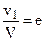в пределах от 0 до 1 и подсчитывая с помощью уравнений (3) и (5), получим следующие значения коэффициентов x_i и В:

Источник

Что такое идеальный ветряк

Теория идеального ветряка, как ее сейчас называют, не создавалась Н.Е. Жуковским специально, а представляет собой вводный параграф к последней из трех статей, посвященных ветрякам, написанных в 1920 году. Внимание к теме ветряков у Жуковского было вызвано предложениями одного изобретателя сулившего огромную мощность от своей ветроустановки. Жуковский имел обыкновение в течение ряда лет вновь и вновь возвращаться к ранее поднятым темам и с присущим ему блеском выяснять суть проблемы до конца. Но последовавшие болезни, смерть любимицы умницы дочери не оставили возможности 73 летнему ученому продолжить работы по данной теме.

Суть теории в следующем.

Когда поток воздуха набегает на вращающийся ветряк, то скорость потока уменьшается. В плоскости ветряка она равна V_в — v₁, а далеко за ветряком V_в — v₂. Работа, производимая ветром, равна разности кинетических энергий набегающего и отходящего воздуха.

(3.1.1)

С другой стороны уменьшение импульса воздушного потока Δp = m₁v₂ = FΔt вызывает силу, воздействующую на лопасти ветряка. Замедленное прохождение воздуха через плоскость ветряка, преодолевающего сопротивление лопастей, вызвано работой, совершаемой ветром.

(3.1.2)

Приравнивая 3.1.1 и 3.1.2 и решая, находим

(3.1.3)

(3.1.4)

То есть замедление скорости ветра за ветроколесом в два раза больше замедления скорости в плоскости колеса.

КИЭВ в данном случае составит величину

(3.1.5)

Максимальный КИЭВ достигается при v₁ = 1/3 V_в и составляет

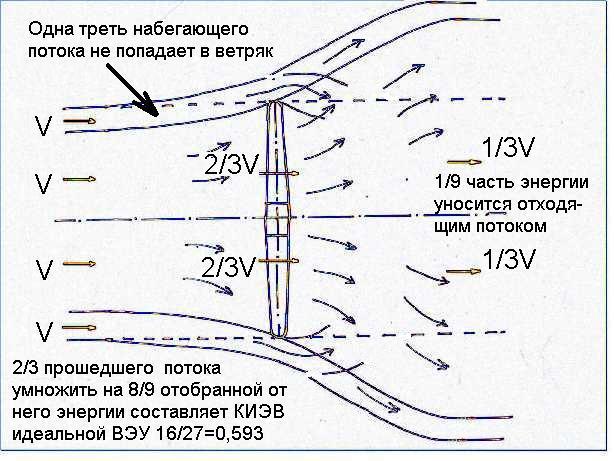
Данная теория, несмотря на ее сугубую абстрактность, является базовой в теории пропеллерных ветроустановок. Поэтому рассмотрим ее более внимательно. Во-первых, обратим внимание на формулу КИЭВ 3.1.5. Скорость потока в плоскости ветроколеса на треть меньше, чем скорость ветра, следовательно, треть набегающего потока не может пройти сквозь ветроколесо и огибает его снаружи. Поэтому в числителе подставлена масса m₁, т.е. масса воздуха прошедшая через ветроколесо, она на треть меньше полной массы m набегающего воздуха, стоящей в знаменателе. Напомню, что воздух в ветроустановках испытывает столь ничтожные давления, что его можно считать несжимаемым. Повышенное давление перед ветроколесом не может служить резервуаром дополнительных масс сжатого воздуха.

Воздух, отходящий в дальней зоне за ветроколесом, имеет скорость в одну треть от скорости ветра, следовательно, он уносит девятую часть энергии потока прошедшего сквозь ветроколесо. Произведение двух третей воздуха, прошедшего сквозь колесо на к.п.д. преобразования энергии, равный восьми девятым и составляет найденный КИЭВ 16/27.

Входящий в формулу 3.1.2 импульс mv₂ позволяет нам сделать важный вывод. Потеря скорости воздухом v₂, а, следовательно, и отдаваемая ветроколесу энергия складывается из двух составляющих. Потери скорости до ветроколеса v₁ и потери скорости после ветроколеса v₂— v₁. До ветроколеса поток теряет треть своей скорости и 5/9 своей энергии, которую передает колесу. После колеса поток теряет еще треть скорости и 3/9 первоначальной энергии. Оставшаяся 1/9 часть энергии уносится отходящим потоком. Понятно, что набегающий поток воздуха создает некое избыточное давление на передней плоскости лопастей, заставляющее вращаться ветроколесо. Поток, находящийся за ветроколесом, может отдать часть своей энергии ветроколесу, оставшемуся позади, только в том случае, если этот поток воздуха, расширяясь, создает разряжение за ветроколесом. Отрицательное давление на задней стороне лопаток увеличивает силу, вращающую ветроколесо. Можно составить уравнения Бернулли и получить те же результаты, что и у Жуковского, оперируя в выкладках понятием давления.

Надо заметить, что теория идеально ветряка не учитывает влияния нескольких факторов: влияние потока воздуха не прошедшего сквозь ветряк, подсоса воздуха в разряжение создающееся за ветроколесом, вращения отходящего воздуха. Не учитываются потери на трение, индуктивные потери, косину набегающего потока. Эти факторы уменьшают КИЭВ. Отходящий медленный поток воздуха считается уходящим в бесконечность. Граница раздела между быстрым внешним потоком и медленным внутренним имеет нулевое сопротивление на трение, т.к. воздух считается идеальной жидкостью. В реальности внешний, быстрый поток смешивается с внутренней струей, ускоряет ее и создает разряжение, которое передается на заднюю сторону ветроколеса. Поэтому КИЭВ должен быть несколько больше. Кроме того, теория идеальногоо ветряка трубует совершенно определенных значений осевой и вращающей силы, действующих на лопасти. Только при этом условии будет получен максимум мощности. Лопасти же работают по своим собственным аэродинамическим законам. И несовпадение энергетических требований ветряка и аэродинамических возможностей лопастей уменьшают КИЭВ. На практике достигнутый КИЭВ равен 43%.

Влияние вращения в отходящей струе нельзя решить количественно в рамках теории идеального ветряка. Эти потери зависят от конкретной реализации ветряка и определяются в ходе практического расчета. Жуковский вывел в той же статье необходимые расчетные формулы реального ветряка. Позже, в результате многочисленных экспериментальных исследований, выяснилось, как пишет проф. Ветчинкин В.П., что характеристика реального ветряка лежит выше найденной Жуковским. Сабинин Г.Х. пытался создать собственную теорию идеального ветряка, но получил по мнению Ветчинкина несколько завышенный результат в 0,687.

Во всем мире данную теорию называют теорией Бетца. Бетц в 1919 году защитил диссертацию, а в 1926 году выпустил замечательную книгу «Энергия ветра и ее использование посредством ветряных мельниц». По воспоминаниям современников в нашей стране вывод идеального КИЭВ впервые сделал в 1914 году Ветчинкин ВП, бывший в то время студентом Жуковского. Скорее всего это студенческое исследование появилось в результате поручения Жуковского. Жуковский любил таким образом побуждать студентов к научной работе. Обнаружить этой работы в Публичной библиотеке в Санкт-Петербурге мне не удалось. Первая письменная работа, посвященная выводу теории идельного ветряка в нашей стране, принадлежит Жуковскому. Датируется февралем 1920 года. Жуковский свой вывод сделал совершенно самостоятельно. Иначе бы он упомянул о Бетце. Николай Егорович был человеком чрезвычайно щепетильным. Петроградский профессор Ботезат Г.А. в 1917 году создал теорию проско-радиального лопастного винта. В теории рассматривались все винты: вентилятора, ветролета, анемомента, тянущий винт. Теорию ветряных мельниц он обещал рассмотреть в следующем издании выпуска, но этого издания не появилось. Шла револющия. Вывод максимального КИЭВ идеального ветряка мало отличается от выкладок при исследовании идеального тянущего пропеллера, которые появились на десятка два лет раньше. Очень вероятно, что подобные расчетные формулы или оценки были получены другими авторами в работах посвященным пропеллеру самолета на рубеже девятнадцатого и двадцатого веков, просто на них, как не имеющих отношения к авиации, не обратили тогда внимания.

Источник